INDICKÉ NÁSOBENÍ

Máme-li např. vypočítat 26 x 7:
- vynásobíme 6 x 7, což je 42, do půleného okénka pod šestku napíšeme
nahoru 4, dolu 2
- vynásobíme 2 x 7, což je 14, do půleného okénka pod dvojku napíšeme
nahoru 1, dolu 4
- nyní sčítáme: 2 není s čím sčítat rovnou jí tedy napíšeme, dále sečteme
4 + 4, což je 8, a 1 není s čím sčítat, tak jí jen opíšeme

- nenásobíme tedy horní čísla mezi sebou, ale vždy jedno horní s jedním
vpravo

Pokud by nám některý výsledek vycházel přes desítku, např. 26 x 9:

- vynásobíme 6 x 9, = 54, napíšeme pod šestku nahoru 5, dolu 4
- vynásobíme 2 x 9, = 18, napíšeme pod dvojku nahoru 1, dolu 8
- sčítáme: 4 není s čím sčítat, jen opíšeme,
8 + 5 = 13, jako při písemném sčítání pod sebe napíšeme jen koncovou
číslovku 3 a jedničku si držíme a přičteme k samotné 1, což je 1 + 1 = 2
- výsledek je 234

ALGEBROGRAMY

Algebrogramy jsou přípravou na počítání rovnic o několika neznámých. Také jsou to ale šifry, které je jednoduché vyluštit, když přijdeme jak na to.
Každé písmenko je vlastně číslo, ale nekdy A může mít hodnotu 2, jindy 4, 20,...
V jednom příkladu však má určité písmenko hodnotu vždy stejnou!

např.
A + A = 10
5 + 5 = 10
A = 5

Pokud se mám objeví dvojčíslo, se stejným písmenkem, pořád má A hodnotu stejnou.
např.

AA + A = 60
55 + 5 = 60
A = 5

Stejně počítáme, i pokud tam máme jiné písmenko - B, T, nebo třeba Ž.
Ž + Ž = 14
7 + 7 = 14
Ž = 7

Pokud máme v příkladu dvě písmenka, má každé jinou hodnotu a příklad může mít více řešení
A + B = 3
2 + 1 = 3 (A = 2, B = 1)
1 + 2 = 3 (A = 1, B = 2)
0 + 3 = 3 (A = 0, B = 3)
3 + 0 = 3 (A = 3, B = 0)

Pokud máme dvojčíslí s dvěma různými písmenky, každé písmenko má svou hodnotu.
např.
AB + A = 15
14 + 1 = 15
A = 1
B = 4
 

OBVOD A OBSAH ČTVERCE A OBDÉLNÍKU

Zatím nepotřebujeme znát žádné vzorečky ani jednotky míry, půjdeme na to chytře a jednoduše

OBSAH (ČTVERCE NEBO OBDÉLNÍKU) = obsah je to, co je uvnitř, spočítáme tedy kolik čtverečků je v celém čtverci/obdélníku.
Např.

Obsah je 9.

OBVOD = obvod je to, co je okolo, musíme tedy počítat dílky okolo celého čtverce/obdélníku.
Např.

Obvod je 12.

SČÍTÁNÍ A ODČÍTÁNÍ S PŘECHODEM PŘES 10

ZVÍŘÁTKA DĚDY LESONĚ

Počítání v tomto matematickém prostředí mi přijde nejjednodušší. K pochopení stačí zapamatovat si hodnotu zvířátek a poznat je dle symbolů.
My zatím pracujeme s pěti zvířátky: myš, kočka, husa, pes, koza.
Zde jsem vypracovala tabulku symbolů a hodnot:

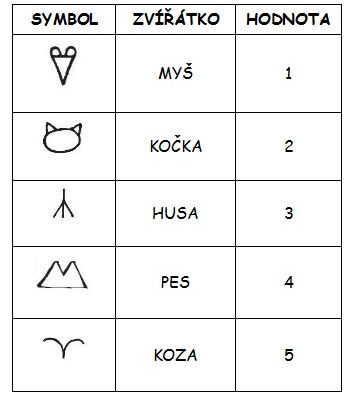
Pokud si zapamatujete symbol zvířátka a jeho hodnotu, máte vyhráno. Zapomeňte také na to, co učili ve škole nás, že jablka a hrušky nemůžeme sčítat :) Protože zvířátka sčítáme dohromady. Hodnota zvířátek, co jsem uvedla v tabulce odpovídá počtu myší, kterému se dané zvířátko rovná:
myš = 1 myš
kočka = 2 myši
husa = 3 myši
pes = 4 myši
koza = 5 myší

Zároveň můžeme zvířátka kombinovat, takže např. husa (3) se může rovnat buď třem myším(1 + 1 + 1), nebo jedné kočce a jedné myši(2 + 1); stejně tak pes (4) se může rovnat buď 4 myším(1 + 1 + 1 + 1), nebo 2 kočkám (2 + 2), nebo 1 huse a 1 myši (3 + 1), atd. 

V učebnici:
- jsme zvířátka rozdělovali do stejně silných družstev, takže zjistíme hodnoty a rozdělíme
- doplňovali jsme zvířátko nebo zvířátka, které má přijít na pomoc slabšímu družstvu, aby byla stějně silná
 

AUTOBUS